7

7. Проекция вектора на ось и ее свойства.

Определение 1. Углом между векторами и называется наименьший угол , на который надо повернуть один из векторов до его совпадения со вторым после приведения этих векторов к общему началу.

называется направленная прямая. Направление прямой на рисунке обычно обозначается стрелкой. Заданное направление оси считается положительным, противоположное - отрицательным.

Рассмотрим ось l, положительное направление которой совпадает с направлением единичного вектора , расположенного на оси l . Такой вектор называется ортом оси l.

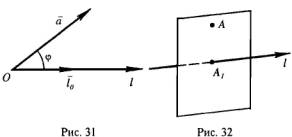
Определение 2. Углом между вектором и осью l называется угол между векторами и (рис. 31).

Определение 3. Проекцией точки А на ось l (рис. 32) называется точка в которой пересекается ось с плоскостью, перпендикулярной к l , проходящей через точку А.

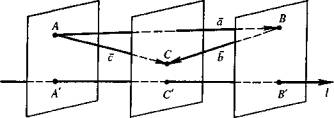
Определение 4 Компонентой (составляющей) вектора = на ось (рис. 33) называется вектор , где , соответственно проекции точек А, В на l .

Определение5. Проекцией вектора на ось l ( ) называется длина его компоненты на ось l , взятая со знаком «плюс», если направление компоненты совпадает с направлением оси l , и со знаком «минус», если направление компоненты противоположно направлению оси .

Если = , то полагают =.

Теорема I Проекция вектора на ось l равна произведению его модуля на косинус угла между этим вектором и осью l.

= .

Доказательство. Так как вектор = свободный, то можно предположить, что начало его О лежит на оси l (рис. 34).

Если угол острый , то направление компоненты = , вектора совпадает с направлением оси l (рис 34,а).

В этом случае имеем = + = . Если же угол (рис. 34, б), то направление компоненты = вектора противоположно направлению оси l. Тогда получаем = = cos( - ) = сos

Наконец, если = (рис. 34, в), то = 0 и соs = 0. Таким образом, снова имеем соотношение = соs.

Следствие1 Проекция вектора на ось положительна, если вектор образует с осью острый угол, отрицательна, если этот угол тупой, равна нулю, если этот угол прямой.

Следствие 2. Проекции равных векторов на одну и ту же ось равны между собой.

Теорема 2. Проекции векторов , на данную ось обладают следующими свойствами:

Доказательство. Свойство (5) иллюстрирует рис. 35. Докажем свойство (6). Считая, что угол между вектором = и направлением l равен , имеем при > О = | |соs = | |соs =

при < 0 = | |соs(- ) = - | |соs ( - ) = | |соs = (при < 0 вектор направлен в сторону, противоположную направлению ; если образует с l угол , то образует с l угол - ). При = 0 левая и правая части (6) обращаются в нуль.

Понятие вектора | Линейные операции над векторами | Понятие линейной зависимости векторов|

Линейная зависимость векторов на плоскости | Линейная зависимость векторов в пространстве

Базис на плоскости и в пространстве | Проекция вектора на ось и ее свойства | Декартова прямоугольная система координат в пространстве| Цилиндрические и сферические координаты| Главная