5

5. Умножение матриц.

Рассмотрим правило умножения двух квадратных матриц второго и третьего порядков. Пусть даны две матрицы

Произведением матрицы А на матрицу В называется матрица С= А В, элементы которой составляются следующим образом:

Как видим, элемент матрицы-произведения, находящийся на пересечении i-й строки и k-го столбца, представляет собой сумму парных произведений элементов i-й строки первой матрицы на элементы k-го столбца второй матрицы.

Например, элемент, стоящий во второй строке и первом столбце матрицы произведения АВ, равен сумме парных произведений элементов второй строки матрицы А на элементы первого столбца матрицы В.

Это правило сохраняется для умножения квадратных матриц третьего и более высокого порядка, а также для умножения прямоугольных матриц, в которых число столбцов матрицы-множимого равно числу строк матрицы-множителя.

Пример1

Пример2

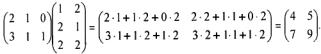
Пример3.

Видим , что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько имеет их матрица-множимое, и столько столбцов, сколько имеет матрица-множитель. Рассмотрим еще пример:

С другой стороны, как установлено выше,

Следовательно, произведение двух матриц, вообще говоря, не подчиняется переместительному закону:

АВ ВА.

Можно проверить, что умножение матриц подчиняется сочетательному закону:

А(ВС) = (АВ)С.

Отметим любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль-матрице.

Пример 4. Если

то

При умножении матриц второго порядка особое значение имеет квадратная матрица

При умножении любой квадратной матрицы

второго порядка на матрицу Е снова получается матрица А.

Действительно,

Аналогично EA =A.

Матрица Е называется единичной матрицей. Единичная матрица n-го порядка имеет вид

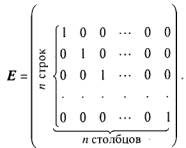
Если в матрице (1), обозначаемой буквой А, сделать все строки столбцами с тем же номером, то получим матрицу

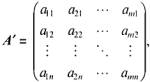
называемую транспонированной к матрице А.