3. Линейная однородная система n уравнений с n неизвестными.
Как уже отмечалось (см. п. 1), система уравнений вида
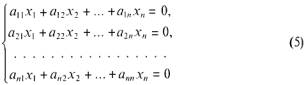
называется однородной. Она является частным случаем
системы
=0,
=0,...,
=0.
Ясно, что эта система имеет нулевое решение
.
Это решение называют тривиальным
решением однородной системы. Но может случиться, что
однородная
система (5) имеет и не нулевое решение. Его
называют нетривиальным решением
однородной системы (5).
Теорема1. Если определитель
однородной
системы (5) не равен
нулю
0), то эта система
имеет только тривиальное решение.
В
самом деле, в силу свойства определителей (см.
§ 2.4., п. 1, свойство 5) все
определители
=
0, поэтому в силу равенств (4)
=0
(i=1,…,n).
Теорема2. Если система уравнений (5) имеет
нетривиальное решение,
то ее определитель
равен
нулю (
= 0).
В
самом деле, если бы
0,
то по теореме 1 система (5) имела бы только
одно тривиальное решение.
Справедливо (см , например, [9]) и обратное.
Теорема3. Если определитель
системы
(5) равен нулю, то эта
система имеет нетривиальное решение.
Матричная запись и матричное решение | Формулы Крамера | Линейная однородная система n уравнений с n неизвестными |
