2. Линейные операции над векторами.
Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число.
Определение. Пусть
и 
два свободных вектора (рис.
26, а). Возьмем произвольную точку О и
построим вектор
=
, затем от точки А
отложим вектор
=
,
Вектор
,
соединяющий начало первого слагаемого вектора с концом второго, называется
суммой этих
векторов и обозначается
(рис.
26, б). Ту же самую сумму
векторов можно получить иным способом.
Отложим от точки О векторы 
=
и 
.
Построим на этих векторах как на сторонах
параллелограмм О ABC Вектор 
, служащий диагональю
этого параллелограмма, проведенной из вершины
О, является, очевидно, суммой векторов
(рис.
26, в). Из рис. 26, в непосредственно
следует, что сумма двух векторов обладает переместительным свойством:
.
Действительно, каждый из векторов
и 
равен
одному и тому же вектору 
.
Понятие суммы векторов, введенное для двух слагаемых векторов, можно обобщить на случай любого конечного числа слагаемых векторов.
Пусть,
например, даны три вектора
,
и 
(рис.
27, а). Построив сначала сумму векторов
,
а затем прибавив к этой сумме вектор
получим вектор
. На рис. 27, б)
= ,
,
,
и
.
Из
рис. 27, б видно, что тот же вектор
мы
получим, если к вектору
=
прибавим вектор
.
Таким образом,
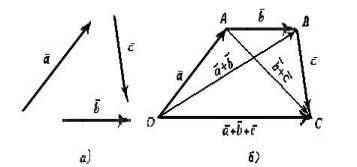
Рис.27
( + ) +
=
+ (
+ ),
т.е. сумма векторов
обладает сочетательным свойством. Поэтому сумму трех векторов
, ,
записывают просто
.
Итак, сумму трех векторов можно получить следующим образом. Из произвольной точки О откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяется начало второго; к концу второго - начало третьего. Вектор, соединяющий начало первого вектора с концом последнего, является суммой данных векторов. Подобным же образом строится сумма любого конечного числа векторов.
Если при сложении нескольких векторов
конец последнего слагаемого вектора совпадает с началом
первого, то сумма векторов равна нулевому вектору. Очевидно, что
для любого вектора имеет место равенство
.
Определение. Разностью
и
называется
третий вектор
, сумма которого с
вычитаемым вектором
дает
вектор
.
Таким образом, если
,
.
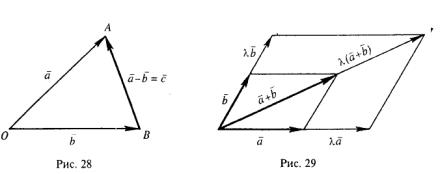
Из определения суммы двух векторов вытекает правило построения вектора-разности (рис. 28). Откладываем векторы
=
и
=
из общей точки О. Вектор
,
соединяющий
концы уменьшаемого вектора
и
вычитаемого вектора
и
направленный
от вычитаемого к уменьшаемому, является
разностью
. Действительно, по
правилу сложения векторов
, или
.
Определение. Произведением 
( или
)
на
,
называется вектор ,
коллинеарный вектору ,
имеющий длину, равную
и то же направление, что и
вектор
, если
> 0, и
направление, противоположное направление
< 0. Так,
например, 2
есть вектор, имеющий то же направление,
что и вектор , а длину, вдвое большую, чем вектор
. В случае, когда
= 0 или
, произведение
представляет
собой нулевой вектор. Противоположный
вектор
можно
рассматривать как результат умножения
вектора
на
Так, западный ветер можно представить
как отрицательный восточный ветер. Очевидно, что
.
Пусть дан вектор . Рассмотрим единичный
вектор
,
коллинеарный вектору
и одинаково с ним направленный. Из
определения умножения вектора на число
следует, что
,
т.е. каждый вектор равен произведению
его модуля на единичный вектор того же направления. Далее из
того же определения следует
=
, где
ненулевой вектор, то векторы
и
коллинеарны.
Очевидно,
что и, обратно, из коллинеарности векторов
и
следует,
что
.
Таким образом, два вектора
и
коллинеарны
тогда и только тогда,
когда имеет место равенство
=
.
Легко убедиться, что умножение вектора на число обладает
и
сочетательным свойством
.
Справедливость, например,
равенства (1) при
следует из того, что при
изменении сторон параллелограмма в
раз в силу свойств подобия его диагональ также
изменяется в
Понятие вектора | Линейые операции над векторами | Понятие линейной зависимости векторов|
Линейная зависимость векторов на плоскости | Линейная зависимость векторов в пространстве
Базис на плоскости и в пространстве | Проекция вектора на ось и ее свойства | Декартова прямоугольная система координат в пространстве| Цилиндрические и сферические координаты| Главная
