:1.Матричная запись и матричное решение системы уравнений первой степени.
Покажем, каким образом мы можем использовать матричный аппарат для решения систем линейных уравнений,
Пусть
дана система из n линейных
уравнений с n неизвестными
:
Числа
называются
коэффициентами
системы(1),
а числа
,
,…,
- свободными
членами. Система линейных
уравнений (1) называется
однородной, если
=
=...=
= 0.
Матрица
называется матрицей системы(1), а ее определитель | А| -определителем системы (1).
Решением
системы(1) называется
совокупность чисел
,
,
которые обращают все уравнения системы в тождества.
Система, имеющая хотя бы одно решение, называется совместной. Система, не имеющая решений, называется несовместной.
Пусть определитель системы (1) отличен от нуля.
Обозначим матрицу-столбец из неизвестных через X и матрицу-столбец из свободных членов через В:
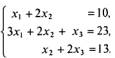
Согласно правилу умножения матриц имеем
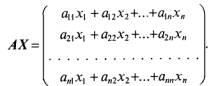
Используя определение равенства матриц, данную систему (1) можно записать следующим образом:
АХ = В.(2)
Равенство (2) называется матричным уравнением (здесь в роли неизвестного выступает матрица X.
Так
как по условию |А|
0, то для матрицы А
существует обратная матрица
. Умножим
обе части уравнения (2) слева на
:
(АХ)
=
В.
Используя сочетательный закон умножения матриц (см. § 2.3, п.5), можно написать
(
А)Х=
В.
Но
так как
А
= Е (см. § 2.4, п. 4) и ЕХ = X(см. § 2.3, п. 5), то получаем
решение матричного уравнения в виде
Х =
B.
Пример. Решить матричным способом систему уравнений:
В матричной форме эта система запишется в виде АХ = В. Здесь
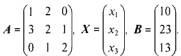
Матрица
была найдена ранее (см. § 2.4, п. 4). Теперь
согласно равенству (3) имеем
Используя определение равенства матриц,
получаем
Непосредственной проверкой убеждаемся, что эти значения неизвестных удовлетворяют данной системе.
Матричная запись и матричное решение | Формулы Крамера | Линейная однородная система n уравнений с n неизвестными |
